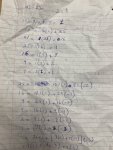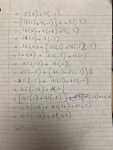Today’s puzzle - معماى امروز
- Thread starter Finally
- Start date
If a subset of {1, 2, 3, ..., 100} can at most have 10 members, the one with the highest sum is:
{91, 92, ..., 100}, with the sum being: (91+100)x5 = 955
So the possible sums for any subset 10 or smaller are: 1 thru 955
Fact: a set of size n, can have (2^n - 1 - n) subsets of size 2 or more. For example:
{a, b, c} can have 2^3 - 1 - 3 = 4 subsets of size 2 or more, namely:
{a,b}, {b,c}, {a,c}, {a,b,c}
So a set of size 10 can have 2^10 - 1 - 10 = 1013 subsets. Because 1013>955, therefore, at least two of these subsets must have the same sum.
(this will be confirmed by any کفترباز who has 1013 pigeons but only 955 pigeon holes in the evening he will have a hole with more than one pigeon in it.)
in the evening he will have a hole with more than one pigeon in it.)
Finally, if two subsets have the same sum but they are not disjoint, you can always remove the common elements and they will still have the same sum,
for example:
{1, 5, 35 } and { 3, 5, 33} have the same sum, 41, but they are not disjoint, we can remove the common element(s), in this example 5, and they will still have the same sum:
{1, 35} and {3, 33}
QED
{91, 92, ..., 100}, with the sum being: (91+100)x5 = 955
So the possible sums for any subset 10 or smaller are: 1 thru 955
Fact: a set of size n, can have (2^n - 1 - n) subsets of size 2 or more. For example:
{a, b, c} can have 2^3 - 1 - 3 = 4 subsets of size 2 or more, namely:
{a,b}, {b,c}, {a,c}, {a,b,c}
So a set of size 10 can have 2^10 - 1 - 10 = 1013 subsets. Because 1013>955, therefore, at least two of these subsets must have the same sum.
(this will be confirmed by any کفترباز who has 1013 pigeons but only 955 pigeon holes
Finally, if two subsets have the same sum but they are not disjoint, you can always remove the common elements and they will still have the same sum,
for example:
{1, 5, 35 } and { 3, 5, 33} have the same sum, 41, but they are not disjoint, we can remove the common element(s), in this example 5, and they will still have the same sum:
{1, 35} and {3, 33}
QED
Last edited:
Likes:
Finally and Payandeh Iran
If a subset of {1, 2, 3, ..., 100} can at most have 10 members, the one with the highest sum is:
{91, 92, ..., 100}, with the sum being: (91+100)x5 = 955
So the possible sums for any subset 10 or smaller are: 1 thru 955
Fact: a set of size n, can have (2^n - 1 - n) subsets of size 2 or more. For example:
{a, b, c} can have 2^3 - 1 - 3 = 4 subsets of size 2 or more, namely:
{a,b}, {b,c}, {a,c}, {a,b,c}
So a set of size 10 can have 2^10 - 1 - 10 = 1013 subsets. Because 1013>955, therefore, at least two of these subsets must have the same sum.
(this will be confirmed by any کفترباز who has 1013 pigeons but only 955 pigeon holes in the evening he will have a hole with more than one pigeon in it.)
in the evening he will have a hole with more than one pigeon in it.)
Finally, if two subsets have the same sum but they are not disjoint, you can always remove the common elements and they will still have the same sum,
for example:
{1, 5, 35 } and { 3, 5, 33} have the same sum, 41, but they are not disjoint, we can remove the common element(s), in this example 5, and they will still have the same sum:
{1, 35} and {3, 33}
QED
{91, 92, ..., 100}, with the sum being: (91+100)x5 = 955
So the possible sums for any subset 10 or smaller are: 1 thru 955
Fact: a set of size n, can have (2^n - 1 - n) subsets of size 2 or more. For example:
{a, b, c} can have 2^3 - 1 - 3 = 4 subsets of size 2 or more, namely:
{a,b}, {b,c}, {a,c}, {a,b,c}
So a set of size 10 can have 2^10 - 1 - 10 = 1013 subsets. Because 1013>955, therefore, at least two of these subsets must have the same sum.
(this will be confirmed by any کفترباز who has 1013 pigeons but only 955 pigeon holes
Finally, if two subsets have the same sum but they are not disjoint, you can always remove the common elements and they will still have the same sum,
for example:
{1, 5, 35 } and { 3, 5, 33} have the same sum, 41, but they are not disjoint, we can remove the common element(s), in this example 5, and they will still have the same sum:
{1, 35} and {3, 33}
QED
Likes:
spinhead
Here's one for your weekend enjoyment:
Prove that there are no two (n by n) matrices A and B such that:
AB - BA = I
where I is the identity matrix.
In other words, equation AB - BA = I has no solution.
You have 168 hours to solve it ...
167:59:59
167:59:58
....
Prove that there are no two (n by n) matrices A and B such that:
AB - BA = I
where I is the identity matrix.
In other words, equation AB - BA = I has no solution.
You have 168 hours to solve it ...
167:59:59
167:59:58
....
Four people come to a river in the night. There is a narrow bridge, but it can only hold two people at a time. They have one torch and, because it's night, the torch has to be used when crossing the bridge. Person A can cross the bridge in 1 minute, B in 2 minutes, C in 5 minutes, and D in 10minutes. The total time befor bridg collapse is only 17 minutiae . Find the solution to the problem.
A and B go and A returns: 2+1 = 3 minutes
A and C go: 5 minutes
Hopefully 9 minutes should be enough to throw the slow D into the river.
Why don't I cut to the chase:
We use two identities:
trace(X + Y) = trace(X) + trace(Y)
trace(XY)=trace(YX)
To show that the trace of the left side is zero:
trace(AB-BA)=trace(AB)-trace(BA)=trace(AB)-trace(AB) = 0
trace of the right side equals n, however, since all diagonal elements equal 1.
So the left side can never be equal to the right side.
We use two identities:
trace(X + Y) = trace(X) + trace(Y)
trace(XY)=trace(YX)
To show that the trace of the left side is zero:
trace(AB-BA)=trace(AB)-trace(BA)=trace(AB)-trace(AB) = 0
trace of the right side equals n, however, since all diagonal elements equal 1.
So the left side can never be equal to the right side.
Without using a computer, find integers a and b such that
41a + 107b = 1
41a + 107b = 1
Hints.... Both are prime, so their largest common divisor is 1. One must be negative and one positive. One must be even, and one odd.
Likes:
spinhead
Hints.... Both are prime, so their largest common divisor is 1. One must be negative and one positive. One must be even, and one odd.
Last edited:
Likes:
spinhead
47 and -18
Hints.... Both are prime, so their largest common divisor is 1. One must be negative and one positive. One must be even, and one odd.
Hints.... Both are prime, so their largest common divisor is 1. One must be negative and one positive. One must be even, and one odd.
I mean, all those statements are true, but they don't tell us how you obtained the answer.
Last edited:
It's like playing hide and seek on planet earth and then to make it easier by restricting it to only northern hemisphere
Both multiples 41 & 107 are prime numbers. So their largest common divisor must be 1. There is a theorem that say, such a solution (integers for both a & b) does exist. I do not remember the name of the theorem.
Now, just looking at the equation, it is easy to deduce what I wrote above; namely that a & b, One must be negative and one positive. One must be even, and one odd. You are right, that does not pinpoint the solution, but should be a starting guide.
Basically, you can think of this equation as an equation of a line, a vs b, where all a and b satisfy the equation. The challenge is to find a set of a &b that are integers. So you can think of drawing this line, and then drawing lines vertical and horizontal for a= Int (for example a=1, a=2 etc)and also b=int (b=1 etc). And then look for places where three lines (41a+107b=1 and a=Int1 and b=Int2) intersect. That is the graphical approach. If you actually draw the graph, you will get an idea of the whereabouts of Int1 and Int1.
Luckily, for the rest of us, some old dude actually worked out an algorithm for doing this. It is based on factoring the two multiples, and working with the remainders to find the solution. I do not remember who it was, but I used his algorithm. I tossed the paper but will see if the trash can still has it. There is a simpler permutation based algorithm (whose inventor I do not recall either) that does the same thing.
Likes:
Payandeh Iran and spinhead